This is a proposal for a geolocation system that was first discussed on the web in a public forum and is herein explained.
A matrix/grid of cubes with an edge of 21 million meters is centered on the center of mass of Earth and oriented along its imaginary axis (North-South), the prime meridian plane and the equatorial plane, with Greenwich/Prime Meridian along the middle of the front. It is a matrix of 9261000000000000000000 (21 million cubed) cubes of one meter cube each. The axis passes on the center of the top and bottom face of the giant cube and the giant cube revolves around it in sync with the planet so that all cubes in the giant grid keep in the same place.
The number 21 million, interestingly, is the limit of BTC that the bitcoin network will ever have in circulation. Interestingly, 21 million cubed has 22 digits. Using such number of digits we are talking not of billions, not of trillions, not of quadrillions, not of quintillions, but of sixtillions number of cubes. A staggering number that is about 30.9 trillion times bigger than the speed of light in vacuum figured on the metric system. This gives a compact, universal, unambiguous and simple way of expressing any geolocation on Earth, that just like a telephone number can easily be told. It encompasses all geolocations on Earth, including the interior and surrounding of it, and it is a size that is good for that purpose. It is roughly the size of a cube of water that had the same mass of the Earth at normal temperature and pressure (NTP [defined as air at temperature: 20°C (68°F) and pressure: 1 atm (Earth's atmospheric pressure at sea level)]).
The order of the cubes is the following: the first cube is closest to the center of our Matrix of cubes, given that we have eight adjacent cubes there; and so the first (cube 0000000000000000000001) must be on what will be our first layer, approaching Greenwich/Prime Meridian, North and West. Then, the second cube, also on our first layer, is the adjacent cube on the right (facing it from the Greenwich/Prime Meridian).
We always go around till we complete the layer.
So facing our matrix of cubes from the Greenwich/Prime Meridian we have the following cube numbers:
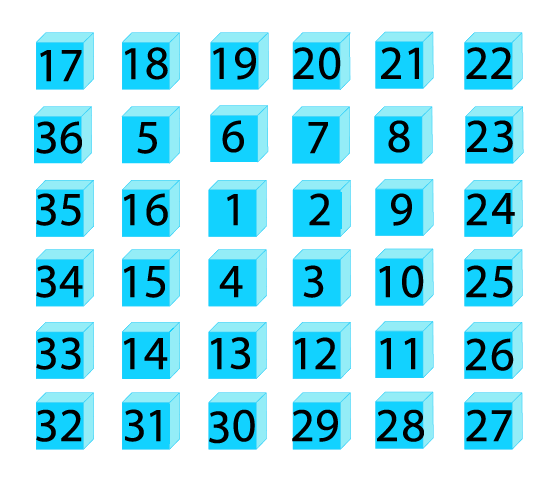

And so on, till the layer is complete and we move on to the center of the next layer, alternating what will be the next layer to make our counting as natural, even and contiguous as possible. The layers in the counting will be alternating as each is completed in the counting process so that the last two layers will be, namely, the closest one to the Greenwich/Prime Meridian and the one more far away from it, similar to the so called Front Face and Back Face of the Rubik's cube. All of our layers are parallel to those last two, obviously.
The cubes are systematically numbered in a spiral pattern, commencing from the center of the planet and expanding outward. To facilitate understanding, visualize a three-dimensional grid where the center pf each cube represents a distinct point in space. The initial layer consists of cubes with their centers positioned precisely at a distance of half a meter from the center of the planet. To precisely locate this layer, we measure the distance in the positive X-axis direction, originating from the planet's center and extending toward the point where the prime meridian (the line denoting zero degrees longitude) intersects with the equator (the line denoting zero degrees latitude). The plane encompassing the centers of these cubes is accurately centered at this half-meter distance. Now, let's delve into the arrangement of subsequent layers. The second layer, considered an even layer, is also situated at a distance of half a meter from the center of mass of the planet. However, an important distinction exists regarding the positioning of layers. Odd-numbered layers, such as the third, fifth, seventh, and so on, are positioned on the positive side of the major axis. Conversely, even-numbered layers, like the second, fourth, sixth, and so forth, are located on the negative side of the major axis. As we progress outward from the planet's center, each odd layer is positioned on one side of the major axis, while each even layer resides on the opposite side. This alternating pattern ensures a systematic distribution of cubes throughout the three-dimensional space. The process of numbering and organizing the cubes continues until all of them have been assigned unique numbers. It is important to note that irrespective of their odd or even status, all layers maintain a consistent vertical orientation. They remain parallel to one another and to the planet itself, adhering to an unvarying alignment. The centers of the cubes in each layer align vertically, following the planet's vertical imaginary axis, and are parallel to the other layers having the plane that contain its centers at a distance of one meter to the ones of adjacent layers (because all the layers have one meter of thickness). By employing this meticulous approach, every cube within this numerical system can be precisely located and identified, forming a comprehensive and structured representation of the planet's spatial arrangement.
The cubes are numbered in this specific way, herein described, and the latitude, longitude and altitude do not directly integrate the 22 numeric digits codes. That creates a stronger case for error detection and for more landmarks/monuments to be put in place making location systems much more resillient, precise, reliable and accurate, edificating the cubes and cubic monuments pharaonlically making them an everlasting part of the planet, resistant to the most adverse conditions and existential risks that we may be unaware of at one moment in time.
A dash may be used to separate the prefix part that will be sufficient for computer systems to give a few auto-complete recommendations of the most likely inhabitable cubes (part of the built environment of humans on that place or surroundings) with such prefix. For instance, if the centre of the cube 7636535637373773383976 was the closest to the door of a residential flat within a few miles from you, but the prefix 7636535637 would restrict enough the possibilities of nearby inhabitable cubes, then the Cubic Postcode would be: 7636535637-373773383976. When typing the cube number in a mobile app, you would need only to type 7636535637 to get a single recommendation in the auto-complete options. The use of a dash to separate the prefix part of the code makes it easier for computer systems to give auto-complete recommendations and can be convenient for instance when posting a letter or using a taxi, promply making it clear the destination without ambiguity.
It is incredible how the "cubic postcode" system can enhance the persistence of VR games and metaverse worlds, allowing us to use the same virtual planet across different platforms. At any time, you can create a large cube by specifying its 8 vertices, and all the cubes within this cubic postcode can be easily listed and transferred to another environment. AI can then adapt these parts of the virtual world to the new platform's game engines. This approach significantly increases the reusability and persistence of worlds and their assets.
This system may reveal itself interesting for real estate where volumetric delimitation is so difficult in any other way. With this proposed system there is no need to define borders using a complicate set of coordinates: you just tell which cubes you are talking about. You can even set a channel in a IRC channel with a cryptographic hash or checksum of a set of sequenced cubes, including if some cubes are in other disjointed areas, using the prefix of that hash for the name of your IRC channel or to create a hashtag for that places that you are talking about. This system may also reveal itself interesting when moving in VR worlds. Imagine saying: "OK Google, cube 9... and as soon as you are saying '9' all cubes that start with '9' are highlighted. And if you would say another digit it would then restrict the number of cubes highlighted, and so on and so forth. If you kept restricting it, the cubes could be so far from you that you could not see them in your field of vision in which case you would see a vector pointing in the direction of its center with the color of that vector representing the distance that such cube is apart from you (ranging from the coolest violet, if it were zero meters apart to the hottest red if it was twenty one million meters apart. Basically you just divide the distance in meters by twenty million meters to get the percentage and find the corresponding color in the visible spectrum of colors, 0% being violet and 100% being red).
So you could be exploring a world using the first digits of cubes to jump from one to another. For instance, if a place reminded you of a specific thing that you liked to explore with cubes that start with 235... you just go on saying "OK Google new cube 235... and it will take you to the closest cube that starts with 235... that you haven't visited before. This way, you could be exploring worlds in a way that you would remember better. For instance, being in a village that makes you think it would be a great place to be in the summer, eating ice cream and with a hat of straw; and it also remembers you of specific friends that used to be around you in summertime during your holidays. This is just an example, naturally many other things could be in your mind, like you could think this would be a great place to live if you were a musician, or any other thing that could cross your mind, for that matter. Whatever you had in mind you could start exploring that world using a specific pattern in the first digits of the next cubes you would pick. So you could just say: "Next 235..." and it would take you to the closest cube that started with 235 in the direction and way you were moving towards. Also you could just say four cubes to make a bezier curve since a bezier curve only needs four points to be specified. The centers of those four cubes would be the four points of your bezier curve. And you could then say the speed at which you wanted that curve to be traveled by. Specifying the bezier curves and their speeds allows one to create trajectories. You could then ask an app like Google Earth to render those travelings at a specific date and time, under any weather/atmospheric circumstances that you wanted... Boom! Just using strings of 22 digits to make bezier curves, deciding the speeds for each of them, etc., and there you were: ready to render real world timelapsing videos as a God-like filmmaker using Google Earth and its state-of-the-art tech.
There is also the real possibility that the spacetime continuum and its dynamic is hyperdimensional and has more than the three spatial dimensions that we live in and that we learn to move physical objects or particles, and waves, into a higher spatial dimension that allow us to observe every single location of the interior of our planet Earth or that we learn to find it out with spiritual development of psychic and/or supernatural abilities and senses we don't have yet developed in the physical universe. There is a great chance that dowsing pendulums using smart tech tracking and communication with supercomputers in a grid with superintelligence (in constant upgrade of data collection, in a multidisciplinary and cutting-edge approach towards better general knowledge systems of analysis and inference using statistics and new and latest discoveries coming from different areas of pure and applied maths) will also allow us to sense and detect the composition of every single cube, in a superiorly resilient fashion ;-)
A possible name for the snake-like set of segments that connect the centers of a set of sequenced cubes could be "cuboid spine". The word "cuboid"
refers to a solid geometric figure that is similar to a cube but may have different lengths, widths, and heights. The term "spine" is often used
to describe a long, thin, and flexible structure that supports and connects different parts of an organism or object. Together, "cuboid spine" could
describe the set of segments that connect the centers of a series of cuboid-shaped objects, resembling the spine of an animal or the
backbone of a structure. Those cuboid spines could be the interest of research for the variety of angles that each two joined segments forms
and its infinite expansions in infininite decimals, possibly of use for the world of computing one day, possibly, since they are there and do exist
in its true nature as if they were set in stone about to be discovered or uncovered by some intriguing curiosity spirit or deep need.
A "natural cuboid spine of order n" is herein defined as: the cuboid spine given its first and last cube numbers and the number of cubes in between, in a list
of n sequenced cubes.
On top of that the system can be extended at a specific time to go ad infinitum to smaller or greater scales "microcubing" or "macrocubing" each cube, like in a fractal that can be travelled both to infnitely wide larger places and to infinite wide smaller places, if you can compute them to the desired scale. It might also be interesting to surf a virtual world using a map of cubes you are familiar with. For instance as you get used to move in your town using AR displaying the Cubic Postcode grid of cubes (each labeled with its 22-digits number) you might then use that map of cubes to surf a different world, positioning it as you want - XYZ - in your reference/map of cubes. This may increase the plasticity of your brain and increase your memory and cognitive function as you will be making your brain flex and interconnect more memories interleaving and superimposing different worlds in different layers/areas of your inner worlds representations.
To summarize and conclude: this is an international postcode system using cubic meters. Each postcode location would be quite small, that is, the size of a cubic meter. Each postcode location would be a meter cube in a grid of cubes with an edge of 21 million cubes. This would total 9,261,000,000,000,000,000,000 cubes. All cubes would be numbered, using 22 algarisms ( {21 Million}3 = 22 digits ).
This would have many applications and particularly cool with augmented reality, semantic web and new ways of world mapping for propriety register and real estate. 9,261,000,000,000,000,000,001 to 9,999,999,999,999,999,999 could be codes used for moving items and cataloguing, like telephone numbers, ISBNs, ISMNs, RFIDs, vehicle licence plates, International Classification of Medications (ICM), International Classification of Diseases (ICD), international advertisments standardized IDs for mainstream and social media to easily reference them using 22 numeric digits hashtags, chess openings and endgames, Rubik's cube positions (note that it has 43,252,003,274,489,856,000 possible combinations, that is, about 43.25 quintillion), citizenship-ID or IP addresses. Everyone would get used to these string codes of 22 algarisms.
It's important to note that the cubes in the range from 9261000000000000000001 to 9999999999999999999999 can be used for any purpose, not just for passports. This range provides a large number of cubes to allocate for various purposes, including passports, license plates, and more. It's up to the governing body or organization to decide how to allocate the cubes within this range for their specific use case. However, it's important to ensure that there is a standardized and universal system in place to avoid confusion and errors.
Many people argue that 22-digits would be hard to remember or communicate without errors. But does anyone know by heart the 16 digits (plus start and expiration dates and security digits) of their credit cards or all the phone numbers in their contacts list? Even without remembering them, it is a simple way of listing them, in a very granular scarce way. Also people argue one cannot make money with this system. But people will be able to create monuments of their favorite cubes and worship them. That can certainly be monetised economically. Also, all sorts of entertainment, contents, theme parks, sanctuaries and reserved areas can be created along the lines of CubicLand, including in the metaverse of concentric planets and stars that we may want to explore. This is a project of great dimension for the whole planet, civilization, and life on Earth. It is a bit like the construction of the Egyptian pyramids. You have to put it into perspective and give it its true dimensions to see the beauty of it and the qualia that it may bring us. It is a whole new wonder on Earth. A whole new scale and standard for the world. Maybe architects can better see the beauty and true dimension of this project and endeavor.
Potential Applications of the Cubic Postcode System
- Augmented reality: Cubic postcodes could be used to create augmented reality experiences. For example, a user could point their phone at a building and see its cubic postcode appear on the screen. The user could then use the cubic postcode to learn more about the building, such as its history, ownership, and current use.
- Semantic web: Cubic postcodes could be used to create a semantic web. The semantic web is a web of data that is linked together using machine-readable metadata. This would allow computers to understand the meaning of data and to make connections between different pieces of data.
- New ways of world mapping: Cubic postcodes could be used to create new ways of world mapping. For example, a cubic postcode could be used to represent a single point on the globe. This would allow for more detailed and accurate maps to be created.
- Propriety register and real estate: Cubic postcodes could be used to create a more efficient and accurate propriety register and real estate system. This would make it easier to track the ownership of property and to make transactions.
- Moving items and cataloguing: Cubic postcodes could be used to track the movement of items and to cataloguing items. This would make it easier to find items and to keep track of inventory.
- Standardized IDs for mainstream and social media: Cubic postcodes could be used to create standardized IDs for mainstream and social media. This would make it easier to identify users and to track their activity.
- Interoperability between games and virtual worlds in the metaverse: Allows a user to select eight vertices to create a cuboid box, which can then be copied and pasted using a 176-digit digital fingerprint. Each vertex is represented by 22 digits, and these digits are combined in crescendo sequence to form the 176-digit fingerprint reference. This fingerprint reference uniquely references the cuboid box within the eight vertices. AI systems can then use this information to recreate that part of the world in a different game or metaverse engine. Furthermore, we can envision a Nvidia and Meta blockchain using NFTs and smart contracts that may create very interesting possibilities in the whole chronology and timeline of the real world.: to start with, the places that are only inhabitable if we use games and virtual worlds of our dear metaverse, living inside it.
- Cubes can be used as door portals, so that going through them one exits one VR metaverse world or game and enters another one. Different users could create different internal wormhole maps, for instance interconnecting their favorite places in a single "metaverse molecule". These special cube portals could be programmed using NFTs and smart contracts, granting privileges to their owners just like with domain name ownership on the web, allowing for redirections and anchoring mechanisms, for instance.
- Create amazing laser shows that rival traditional fireworks displays. These shows can highlight the lines of the cubic postcode 3D lattice in impressive ways, fostering new cultural phenomena among animals and wildlife through the subtle influence of feminine dominance inherent in all biological systems.
Note that, no matter where you are on the globe, if you are able to see the edges of the cubes with AR, the cubes where you are will have a special alignment with the Sun, at noon time in London, by Big Ben, (GMT).
The author of this model, Mr. Cubic Postcode, a lusofranco Portuguese-British with strong nordogermanic connections and an anglosaxophonic influence, mainly jazzistic/bluenote, with a Bachelor in Computers Engineering from the London South Bank University - living in London - admits this model and system of geolocation may have had inspiration and influence from The Matrix and Cube movies and vice-versa; and also from the Rubik cube toy and Minecraft videogame.
The number 42 - considered by many people a peculiar number with a special place in literature and maths and even the name of a very
well known and successful university in France [https://www.42.fr] that seems to be expanding into an international online school for
the serious geek - is also ten factorial divided by the number of seconds in a day. This mysterious discovery is to be attributed to Daniel Alexandre.
Note also that an average game of chess lasts for about that number of moves!
He is also most well known for his radical activism against bloody bullfighting and vigorous support for animal rights and their well-being.
He wrote a manifesto on that subject that was published as a book with ISBN: 972-9098-50-6.
And, of course, you can use a 22-digits Cubic Postcode cube as a #hashtag to tell where about you are or are talking about. Like this one: #3141592653589793238462 (https://www.google.com/maps?q=-47,-66) inspired in the number Pi: 3.?4?5...
Also, the hypocenters of earthquakes may be referenced with their cubes.
Mr. Cubic has certainly a high profile (at least much higher than the average folks) for being Satoshi Nakamoto - the mysterious creator of bitcoin - since he is a
computer scientist (able to read RFC documents) and OOP programmer
(with a decent knowledge of Concurrency, Multithreading, Basic Networking with sockets and its ports, TCP/IP vs. UDP protocols, and Design Patterns)
and did file a patent in the UK in 2007 related to 'digital cash money' that shows some insight into the future and inception of bitcoin
[Link 1].
Also, his PayPal account handle is: 'mymondex' which relates to a Mastercard technology (back in 2007) along ideas of a New World Order.
Back in 2006, when he was graduating in Electronics he got particularly interested in the Austrian School of Economics, and very fond of the book "The Mystery of Banking", by Murray N. Rothbard, as you can see in the records of his very experimental and bat sh!t crazy websites still available (to a certain extent) on the "Wayback machine at archive.org" [Link 2]
This mate, Mr. Cubic, with his legal name being Cubic Postcode, knows what is a mutex and has used it in the programming language Pascal, preferred by his professor of Concurrent Systems, Robert. As a side note, he never used Pretty Good Privacy at University. It seems a bit of a joke, but it is true.
He is a legendary user of the Bitcoin Forum with thousands of posts under two different user accounts, where he digresses about many things like his little protocol to encode bitcoin addresses using only numbers, that he snugly named: 'Bitcoin Morse' [Link 3]. Or his theory for the evolution of a brain that has a special ability to recognize the salient features of the (3,4,5) Pythagorean triple, where five is the hypotenuse correponding to less pleasant half-tones. There is no other sound reason or better explanation for why our brains evolved to perceive so well the 12 halftones in between the doubling of sound frequency that constitutes the musical octave. He is fascinated with the (3,4,5) triple, saying that we should be worshiping it to the Cosmos, namely with a Dyson sphere pulsing that pattern in loop (Off, On, Off, On, Off, On, Off, Off, On, Off, On, Off, On, Off, On, Off, Off, On, Off, On, Off, On, Off, On, Off, On, Off. That is, looping cycles of 27 seconds interpolating On and Off, totalling 3200 cycles a day). [Link 4].
But, as we all know, Satoshi Nakamoto does not want to reveal himself as the creator of bitcoin and would rather let it be an enigma. Which must be respected, as much as possible.
The cubic postcode is a revolutionary concept that has the potential to change the way we locate and track objects on the planet. At its core, it involves the use of solid cubes with telescopic arms that can extend to high altitudes and provide accurate location data with great precision. These cubes can be connected using metric grids of lasers and lights, making them highly visible at night and allowing for easy tracking of their location. One of the primary benefits of the cubic postcode is its potential to improve road safety and self-driving viability. By providing more accurate location data than current GPS systems, it could help to prevent accidents and make autonomous vehicles more reliable. It could even eventually allow us to track the movement of all animals, including precise traits of human body language in walking, sports, and the performing arts. But the potential applications of the cubic postcode don't stop there. It could also serve as a valuable tool for geologists, providing highly accurate information about the movement of tectonic plates and the occurrence of earthquakes. The four bottom vertices of each cube could have sharp pendulums with sensors pointing to the center of mass of the planet, registering any changes even when minimal. Additionally, the cubic postcode could be used as highly accurate weather stations, analyzing things like wind, humidity, temperature, air pressure, and precipitation with great precision. This could have significant implications for weather forecasting and climate research. In terms of architecture and aesthetics, the cubic postcode also has potential. The cubes could be located in precise places and connected with grids of lasers and lights, creating beautiful and amazing light shows around the physical monuments. This could potentially enhance the beauty of cities at night and provide new opportunities for creative expression. One of the most impressive aspects of the cubic postcode is its potential for accuracy and standardization. The grid can be divided into millimetric cubic cells of any minuscule size required, providing highly precise and standardized location data. Overall, the cubic postcode is a fascinating concept with enormous potential. While there are still many technical challenges to overcome, the potential benefits for geology, astronomy, weather forecasting, road safety, self-driving cars, and more are significant. It will be exciting to see how this technology develops in the coming years and how it could transform our world. Location addressing has come a long way since the introduction of street names and house numbers. However, traditional addressing systems are often confusing and prone to error, especially in densely populated areas or locations with multiple buildings or units. This is where Cubic Postcode comes in, offering a new and innovative approach to location addressing. Cubic Postcode is a location addressing system that uses a unique combination of two digits and five well-known words from a list of 9999 words to address a specific cube. The system was crafted by AI systems after careful consideration of more than 200 languages, dialects, and accents, along with other details related to the cubes of Cubic Postcode. The use of popular English words from a carefully crafted list of 9999 words offers several benefits over traditional addressing systems. For one, the use of well-known words makes it easier for people to remember and communicate their location. It also eliminates the need for long and complex alphanumeric codes, making it more accessible to a wider range of people, including those who may have difficulty remembering or pronouncing numeric digits. Cubic Postcode is a 3D system that includes all locations, both inside and outside the planet, at the altitude of most satellites, such as those used by the Starlink network. The system is designed to be highly accurate, with each cube measuring just one cubic meter (a side of one meter). This means that Cubic Postcode can be used to address any location with pinpoint accuracy, from a specific building or unit to a precise outdoor location. One of the key benefits of Cubic Postcode is its flexibility. The system can be used to address any location, whether it's a residential or commercial property, a landmark or tourist attraction, or even a specific point on a hiking trail or outdoor adventure. This makes it ideal for a wide range of applications, including emergency services, delivery services, and navigation apps. The use of popular English words from a carefully crafted list of 9999 words also makes Cubic Postcode highly adaptable to different languages and cultures. The list of words was carefully chosen to be widely known and used in different parts of the world, ensuring that the system is accessible to a global audience. In addition, Cubic Postcode has the potential to be used in a wide range of other applications, including telephone numbers, mobile phone indexing, and more. By incorporating Cubic Postcodes into telephone numbers, for example, people could potentially remember and verify the correct phone number more easily. By indexing mobile phones to cubes based on the main residence of the main user, the phone could offer location-specific features and recommendations that are tailored to the user's preferences and interests. In conclusion, Cubic Postcode is a game-changer in the world of location addressing. Its use of popular English words from a carefully crafted list of 9999 words, along with its 3D system and pinpoint accuracy, makes it an ideal solution for a wide range of applications. With its potential for global adoption and standardization, Cubic Postcode has the potential to revolutionize the way we think about location addressing and navigation. In conclusion, the CubicPostcode system presents a revolutionary approach to addressing and locating geographical coordinates worldwide. The incorporation of artificial intelligence can significantly enhance the efficacy of this system by intelligently numbering the cubes based on their geographical clusters and relevance to the built environment. Collaborating with cutting-edge AI organizations like Google DeepMind will enable the development of advanced algorithms that accurately and efficiently assign cube numbers, taking into consideration factors such as proximity to essential infrastructure, population density, and socio-economic dynamics. This innovative approach will not only optimize the ease of navigation but also create opportunities for improved urban planning, resource allocation, and emergency response, ultimately leading to a more interconnected and smarter world.
Since “Vitruvian Man” fits a sphere with a diameter of 222.2 millimeters, we define the "reference humanoid cube" as the smallest cube that can contain this sphere. Initially, this cube has a side length of 2.2 meters. However, considering the cubic postcode uses the number 21 million, we adopt a side length of 2.1 meters for the reference humanoid cube, making each of its cubic cells 100 nanometers (0.1 μm). A humanoid inside this cube would have equal space below the feet and above the head, centering the smallest box that can fit it. The reference humanoid cube is a theoretical construct representing the average human body, with a side length of 2.1 meters. This cube is divided into cubic cells, each 100 nanometers (0.1 μm) on a side, allowing a humanoid to be centered with equal space above and below. This tool is used for visualizing the human body and understanding its interaction with the environment, and is applied in computer graphics, robotics, and architectural design. In computer graphics and animation, it helps create realistic human models. In robotics, it aids in designing robots that safely and efficiently interact with humans. In architecture, it assists in designing buildings that are comfortable and accessible. For the standard "skin" of a humanoid within the reference humanoid cube, each cubic cell represents a control point with specific degrees of freedom. The control points should be minimal yet evenly distributed to allow free movement in all directions. Rotational degrees of freedom for each cell can be assigned using Euler angles (roll, pitch, yaw) or other mathematical representations like quaternions or transformation matrices. The ranges of movements for each control point must align with the humanoid's design limitations and capabilities. The standard "skin" should be compatible with various exoskeleton skins to provide flexibility and functionality. This approach involves defining a coordinate system within the reference humanoid cube and assigning degrees of freedom to control points, forming the basis for the standard humanoid "skin." Exoskeleton skins can then interact with these control points to offer additional features. By following these guidelines, an effective and efficient standard "skin" for a humanoid can be established.
The same system of giant grid of cubic cells can be used in the macrospic and microspoic world, at any scale conceivable or computable for any given complexity system that is the object of our study.
For instance, in Astronomy, for the solar system you could consider the smallest astronomical giant cube that can fit all of the 9 planets of the solar system and its moons, with the direction of resulting vector of the angular moment of that whole mechanical system to be aligned with the direction of its main vertical imaginary axis, and then dividing the cube in our grid of 9.261(^e+21) imaginary cubic cells.
For a galaxy one could consider the smallest cube that can fit all of its stars and center that reference giant cubic grid in the center of mass of the whole system and orient it also using its angular momentum
vectorial direction. This could prove useful to Science and our whole Civilization technology making systems more resillient,
precise, reliable and accurate.
Benefits of Using an Edge Length of 21 Million Units for the Reference Cube
- Universal Standard:
- Establishing a standardized edge length of 21 million units for the reference cube creates a universal and consistent reference point for various systems to interoperate.
- This standardization enables seamless communication and interoperability between different applications, industries, and scientific disciplines that utilize the reference cube.
- Scalability:
- The edge length of 21 million units provides scalability to accommodate a wide range of applications and systems.
- The cube's size is suitable for representing diverse objects and phenomena across different scales, from microscopic to macroscopic.
- This scalability allows for the reference cube to be applied in various fields, including astronomy, biology, robotics, and architecture, among others.
- Compatibility and Interchangeability:
- Since the reference cube is established as a standard, systems and models developed using it can be easily shared, integrated, and exchanged between different platforms and applications.
- This compatibility and interchangeability foster collaboration and facilitate the development of complex systems that rely on consistent and shared mathematical properties.
- Mathematical Properties:
- The mathematical properties of the reference cube, such as its evenly divided cubic cells and the ability to define degrees of freedom within these cells, provide a structured framework for analysis, simulation, and modeling.
- These properties enable precise calculations, measurements, and comparisons within the reference cube, contributing to the accuracy and reliability of the systems that utilize it.
- Research and Development:
- The establishment of the reference cube with an edge length of 21 million units creates a focus for research and development efforts.
- Scientists, engineers, and researchers can explore the implications and applications of this standardized reference, leading to advancements in various fields.
- The reference cube becomes a common language and framework for interdisciplinary collaboration and innovation.
Overall, the use of an edge length of 21 million units in the reference cube offers a universal and standardized reference point that facilitates interoperability, scalability, compatibility, and mathematical precision. It provides a foundation for systems to communicate and interact seamlessly, promoting advancements in research, technology, and scientific understanding across diverse domains.
# Author: Mr. Cubic Postcode, BEng (Hons). This work is licensed under a Creative Commons Attribution 4.0 International License. # To view a copy of this license, visit https://creativecommons.org/licenses/by/4.0/legalcode. # Collaboration: Vyacheslav Sokolov (https://github.com/TheOsch) & Houcem Chlegou (https://github.com/chesedo) # Used resources: # 1) https://en.wikipedia.org/wiki/ECEF and https://en.wikipedia.org/wiki/Geographic_coordinate_conversion # 2) https://oeis.org # cube is the cube number without leading zeros. Enter required value, manually! # change for whatever you want; 22 digits cube without leading zeros cube = 3141592653589793238462 # Inspired in PI number. Change to desired cube! a = 441000000000000 # a is the constant number of cubes in one layer. And last cube in first layer cube_projection = (cube % a) # The cube projected on a cube on the first layer. We use the modulus operation. Simple. half_of_1 = (1/2.0) n_squareference = (((cube_projection - 1) ** half_of_1) / 2) + 1 # n_squareference is the squareference index number. n_squareference = int(n_squareference) # Let's calculate the numbers of cubes in the top-right, bottom-right and bottom-left corners # of the square number n_squareference right_top = (2 * (n_squareference - 1)) ** 2 + 2 * n_squareference right_bottom = right_top + 2 * n_squareference - 1 left_bottom = right_bottom + 2 * n_squareference - 1 # Calculate the Y coordinate if cube_projection >= right_top and cube_projection <= right_bottom: Y_meters = n_squareference elif cube_projection >= left_bottom: Y_meters = -n_squareference + 1 elif cube_projection < right_top: Y_meters = cube_projection - right_top + n_squareference else: # if cube_projection > right_bottom and cube_projection < left_bottom Y_meters = right_bottom - cube_projection + n_squareference Y_meters -= 0.5 # Calculate the Z coordinate if cube_projection <= right_top: Z_meters = n_squareference - 1 elif cube_projection >= right_bottom and cube_projection <= left_bottom: Z_meters = -n_squareference elif cube_projection < right_bottom: Z_meters = right_top - cube_projection + n_squareference - 1 else: # if cube_projection > left_bottom Z_meters = cube_projection - left_bottom - n_squareference Z_meters += 0.5 n_layer = cube / a n_layer = int(n_layer) n_layer += 1 if ((n_layer % 2) != 0 ): # if n_layer is odd X_meters = n_layer / float(2) # The XYZ_earth X coordinate in meters if layer is odd if ((n_layer % 2) == 0 ): # if n_layer is even X_meters = - (n_layer - 1) / float(2) # The XYZ_earth X coordinate in meters if layer is even print('X_meters: ' , X_meters) print('Y_meters: ' , Y_meters) print('Z_meters: ' , Z_meters)
# Author: Mr. Cubic Postcode, BEng (Hons). This work is licensed under a Creative Commons Attribution 4.0 International License. # To view a copy of this license, visit https://creativecommons.org/licenses/by/4.0/legalcode. # Collaboration: Vyacheslav Sokolov (https://github.com/TheOsch) from sys import argv def coord_round(x): return int(x) if x >= 0 else int(x) - 1 # X, Y, Z are the coordinates of a point in ECEF cooredinate system. # Provide them in a command line ('python xyz2code.py [X] [Y] [Z]') # or change default values here if len(argv) == 4: X = float(argv[1]) Y = float(argv[2]) Z = float(argv[3]) else: # These values result in the postal code 3141592653589793238462 # (inspired by the Pi number) X = 3561896.5 Y = -8402969.5 Z = -9767161.5 # Transfer the float coordinates to integers. (x, y, z) = (coord_round(coord) for coord in (X, Y, Z)) print('x, y, z =', x, y, z) # Let's agree upon some terms: # # Layer - a set of cubes sliced by X. 1st Layer is a set of cubes where X in [0, 1); # 2nd Layer - [-1, 0); 3rd - [1, 2); 4th - [-2, -1) etc. A number of Layer is # determined by X coordinate and nothing else. The postal code is ordered by # layer by layer. Each layer contains 21 million * 21 million = 441000000000000 # cubes. In other words, a layer number is a postal code divided by 441000000000000. # Projection - a projection of a particular layer to layer 1. For example, a projection of # cube 441000000000001 is cube 1; a projection of cube 882000000000123 is cube 123. # In other words, a projection is a remainder of division of postal code # by 441000000000000. # A number of cube in a projection is determined by Y and Z but not X # Square - a set of cubes in projection that form a particular squareference. # For example, square 1 is cubes 1,2,3,4; # square 2 is cubes 5-16; suare 3 is cubes 17-36 and so on. # First, let's find a square number. # The square consists of 4 sides: top, left, right and bottom. All the cubes in left and right # sides have the same Y coordinate (negative on the left side and positive on the right side, # but the absolute values are the same. So do top and bottom sides, but the coordinate is Z. # Thus, the square number is just one of the point's coordinates, Y or Z. Which one? # Obviously: the Y coordinate can't be more than the coordinate of the right side and less than # the coordinate of the left one; so do Z coordinate, top and bottom sides. # Thus, the square number is just a maximum of absolute values of Y and Z square_number = max(y + 1, z + 1, -y, -z) print('square_number =', square_number) # Now we need to calculate the numbers of cubes in the top-left, top-right, bottom-right # and bottom-left corners of the square we found left_top = (2 * (square_number - 1)) ** 2 + 1 right_top = left_top + 2 * square_number - 1 right_bottom = right_top + 2 * square_number - 1 left_bottom = right_bottom + 2 * square_number - 1 print('corners =', left_top, right_top, right_bottom, left_bottom) # Now let's find a number of a cube in the projection if square_number == - y: # left side if square_number == z + 1: # top-left corner cube_p = left_top else: cube_p = z + left_bottom + square_number elif square_number == y + 1: # right side cube_p = right_top + square_number - 1 - z elif square_number == z + 1: # top side cube_p = right_top - square_number - y else: # square_number == - z, bottom side cube_p = right_bottom + square_number - y print('cube_p =', cube_p) # Now let's find layer number (decreased by 1 - we need the first layer to have a number 0) if x >= 0: layer_number = x * 2 else: layer_number = -x * 2 - 1 # Let's join them code = layer_number * 441000000000000 + cube_p # That's all print('code =', code)
# Author: Mr. Cubic Postcode, BEng (Hons). This work is licensed under a Creative Commons Attribution 4.0 International License. # To view a copy of this license, visit https://creativecommons.org/licenses/by/4.0/legalcode. # Collaboration: Vyacheslav Sokolov (https://github.com/TheOsch) # Converts between GPS coordinates (Latitude-Longitude-Altitude) and X-Y-Z cartesian coordinates, or vice versa # The cartesian coordinate system is a right-hand, rectangular, three-dimensional, # earth-fixed coordinate system with an origin at (0, 0, 0). # The Z-axis, is parrallel to the axis of rotation of the earth. The Z-coordinate is positive # toward the North pole. # The X-Y plane lies in the equatorial plane. The X-axis lies along the intersection of the plane # containing the prime meridian and the equatorial plane. # The X-coordinate is positive toward the intersection of the prime meridian and equator. from __future__ import print_function import math RADIUS = 6378137 FLATTENING_DENOM = 298.257223563 def FLATTENING(): return 1 / FLATTENING_DENOM def POLAR_RADIUS(): return RADIUS * (1 - FLATTENING()) def RADIUS_SQRT(): return RADIUS * RADIUS def POLAR_RADIUS_SQRT(): return POLAR_RADIUS() * POLAR_RADIUS() def ECCENTRICITY2(): return (2 - FLATTENING()) * FLATTENING() def ECCENTRICITY(): return math.sqrt((RADIUS_SQRT() - POLAR_RADIUS_SQRT()) / RADIUS_SQRT()) def ECCENTRICITY_PRIME(): return math.sqrt((RADIUS_SQRT() - POLAR_RADIUS_SQRT()) / POLAR_RADIUS_SQRT()) print(RADIUS) print(FLATTENING_DENOM) print(FLATTENING()) print(POLAR_RADIUS()) def LLAToECEF(lat, lon, alt=0): print(lat, lon, alt) rlat = lat / 180 * math.pi rlon = lon / 180 * math.pi slat = math.sin(rlat) clat = math.cos(rlat) N = RADIUS / math.sqrt(1 - ECCENTRICITY2() * slat * slat) x = (N + alt) * clat * math.cos(rlon) y = (N + alt) * clat * math.sin(rlon) z = (N * (1 - ECCENTRICITY2()) + alt) * slat return [x, y, z] def ECEFToLLA(X, Y, Z): p = math.sqrt(X * X + Y * Y) theta = math.atan((Z * RADIUS) / (p * POLAR_RADIUS())) sinTheta = math.sin(theta) cosTheta = math.cos(theta) num = Z + ECCENTRICITY_PRIME() * ECCENTRICITY_PRIME() * POLAR_RADIUS() * sinTheta * sinTheta * sinTheta denom = p - ECCENTRICITY() * ECCENTRICITY() * RADIUS * cosTheta * cosTheta * cosTheta latitude = math.atan(num / denom) longitude = math.atan(Y / X) N = getN(latitude) altitude = (p / math.cos(latitude)) - N if X < 0 and Y < 0: longitude = longitude - math.pi if X < 0 and Y > 0: longitude = longitude + math.pi return [degrees(latitude), degrees(longitude), altitude] def getN(latitude): sinlatitude = math.sin(latitude) denom = math.sqrt(1 - ECCENTRICITY() * ECCENTRICITY() * sinlatitude * sinlatitude) N = RADIUS / denom return N def degrees(angle): return angle * (180 / math.pi) [X, Y, Z] = LLAToECEF(10, 12, 20) print([X, Y, Z]) print(ECEFToLLA(X, Y, Z))
